V posledních letech se autonomní navigace bezosádkových prostředků stala jednou z dynamicky se rozvíjejících oblastí výzkumu, kde tento rozvoj již od počátku milénia významně akcelerovala Americká agentura pro pokročilé obranné projekty (DARPA) prostřednictvím mnoha soutěží v dané oblasti. V komerční sféře se očekává, že autonomní vozidla způsobí průlom v osobní i nákladní dopravě a také resorty obrany si uvědomují, že se jedná o klíčový technologický komponent robotizovaného bojiště, umožňující nasazení obrovského počtu vysoce koordinovaných pozemních systémů. V tomto kontextu pak hraje klíčovou roli při vývoji, testování a navyšování schopností algoritmů autonomního řízení fyzikální vozidlová simulace.

Jedním z klíčových oblastí pro efektivní operační nasazení robotizovaných prostředků ve vojenství je logistika, průzkum, eliminace výbušných zátarasů a v neposlední řadě i bojová činnost. V rámci všech těchto oblastí je nutné neustále řešit proces autonomního pohybu robotizovaných pozemních prostředků v komplexním prostředí a jejich efektivní koordinaci. 

Obecně je problém nalezení optimální trasy vojenských UGV (Unmanned Ground Vehicle – pozemní bezosádková vozidla) charakterizován minimalizací tzv. „taktické ceny“ představující úsilí nebo obtíže při překonání úseku z výchozího postavení do cílové destinace. Klíčovými komplikacemi při výpočtu daného manévru je jednak fakt, že počet kombinací manévru vedoucího do cílové destinace může být teoreticky nekonečný (pokud neuvažujeme vozidlo pohybující se na kolejích) a také, že daný manévr může respektovat nekonečný počet rychlostních průběhů, která mají diametrální vliv na výpočet hodnocení zmíněné „taktické ceny“ manévru. K tomu, aby byl problém vůbec řešitelný, se používá celá řada transformací, aproximací, diskretizací, algoritmů a dalších přístupů, vedoucích k již poměrně dobře zvládnuté „teoretické“ řešitelnosti dané úlohy. Hlavní komplikací zůstává jednak jistá míra neurčitosti v procesu výstavby „digitálního dvojčete“ okolního prostředí pramenící z potřeby vysoce komplexní senzorické báze a jejího obtížného dosažení, a zejména výpočetní náročnost optimální trajektorie UGV v reálném čase. Ukazuje se, že informace z běžně používaného segmentu senzoriky, jako jsou RGB kamery a zařízení využívající metodu LIDAR (metoda dálkového měření vzdálenosti na základě výpočtu doby šíření pulsu laserového paprsku odraženého od snímaného objektu), či dalších systémů pro navigaci v off-road prostředí, zdaleka nestačí a je nutné je doplnit o další senzory (radarové, zvukové, multi/hyperspektrální apod.).

Jak již bylo zmíněno, „kostra“ (architektura) algoritmu autonomní navigace je v obecné rovině dobře popsána a jeho možná zjednodušená interpretace je znázorněna na následujícím obrázku:

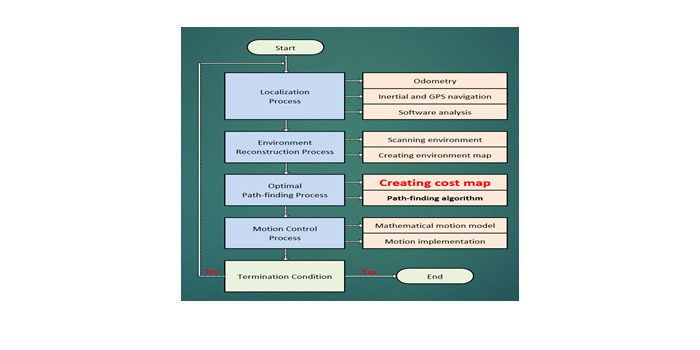
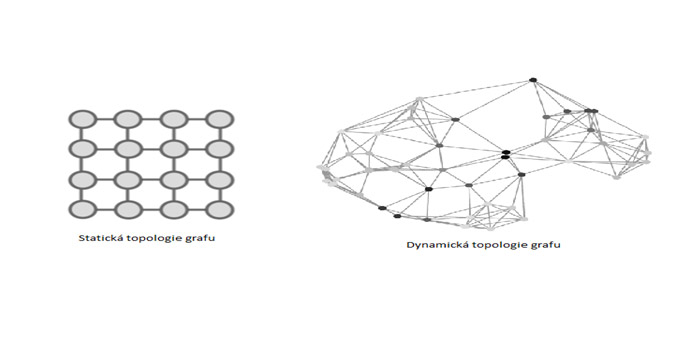
Vynecháme-li komplexní průhled do problematiky výpočtu globální a lokální trasy, včetně sebelokalizace, můžeme obecně říci, že za současného stavu poznání je stěžejní částí celého problému řešení optimální trajektorie výpočet tzv. taktické „cost mapy“, tedy ohodnoceného matematického grafu manévru, ovlivněný celou řadou dalších okolností, na který je obvykle aplikován algoritmus hledání minimální cesty. Výstavba grafu manévru může probíhat buď s jeho předem definovanou topologií (statická), nebo s adaptivním rozložením uzlů a spojů vyvíjejících se dle aktuální situace a možností manévru v okolním prostředí (dynamická), jak je znázorněno na následujícím obrázku. Dynamická topologie skýtá řadu výhod ale i komplikací. Primárně však umožňuje datovou a výpočetní úsporu úsilí na oblasti terénu (území), kde nalezení trasy optimálního manévru je nejvíce pravděpodobné.

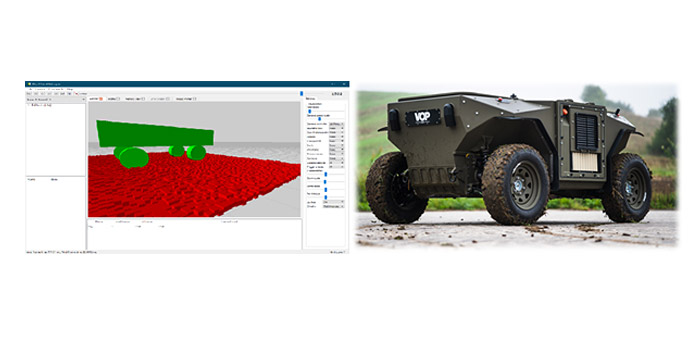
Dalším krokem je ohodnocení manévrového grafu, což je výpočet „operační efektivity“ přesunu mezi jednotlivými uzly grafu (reprezentující jednotlivé body v prostoru), kde se jako ideální jeví využití metody fyzikální simulace vozidla v modelu prostředí, které bylo vytvořeno z dostupných senzorů na vozidle, včetně integrace informace z vyšších systémů velení a řízení.

Ukazuje se, že celková kvalita a spolehlivost automatického řízení závisí z velké míry na dostatečné korelaci simulace s reálným průběhem jízdy vozidla (High Fidelity Simulation), což se v kontextu potřeby značného počtu parciálních simulací jeví jako problém volby jistého  kompromisu, který se řeší aproximací geometrické konstrukce vozidla, volby simulačního „solveru“ a případně heuristických přístupů vedoucích k rychlému zamítnutí neperspektivních směrů pohybu vozidla, a tedy značné úspory výpočetního času. V současnosti se na Katedře vojenské robotiky na Univerzitě obrany zaměřujeme na zkoumání a využití variace fyzikálních simulačních RBS (Rigid Body Simulation) a MBS (Multi Body Simulation) přístupů, které by měly přinést významné navýšení spolehlivosti tzv. „manévrového grafu“, včetně „relativně přesného“ výpočtu maximálního rychlostního profilu, který je možné na dané trase bezpečně aplikovat.

Přístup k celkovému řešení výstavby topologie manévrového grafu, kterým se zabývá Katedra vojenské robotiky, je orientován v daném ohledu do obou směrů, a to jak na výstavbu statického grafu s hustou strukturou možností potenciálních směrů manévru, což se jeví v současnosti jako výpočetně (v reálném čase) zvládnutelné, tak na perspektivní směr výstavby adaptivního tzv. RET (Rapidly Expanding Tree) případně RRT (Rapidly Exploring Random Tree) grafu respektující buď všechny nebo všechny perspektivní možnosti manévru daného prostředku do předem definované úrovně. Bohužel rychlost růstu prvně zmíněného grafu (RET) je exponenciální a dosahuje mezní hranice toho, čeho jsou současné nejvýkonnější výpočetní systémy schopny v reálném čase zvládnout (což je mimochodem pro adekvátní řešení nedostatečné).

Daný fakt ukazuje, že se jedná o zásadní problém, jehož vyřešení přinese určitou revoluci do celého segmentu autonomního řízení. Jako analogii můžeme uvést například oblast rasterizace versus raytracingu z oblasti počítačové grafiky, kde raytracing výrazně zjednodušuje celý proces řešení (2D) vizualizace 3D scény. Raytracing je však velmi náročný na výpočetní výkon a ačkoliv jeho aplikační počátky sahají do šedesátých let minulého století, grafické karty schopné tento proces řešit v reálném čase se na trhu objevily až po roce 2020.

Z tohoto důvodu je daná oblast předmětem intenzivního zkoumání, zejména v kontextu integrace dalších heuristických metod, a předpokládá se, že potřebný HW, schopný zvládnout daný objem výpočtů v reálném čase (instalovaný na vozidle), se na trhu objeví až za několik let.